Novel one-dimensional nanopatterns on vicinal Cu(001)-c(2x2)N surfaces

Shin-ya Ohno, Kan Nakatsuji Kazuma Yagyuu and Fumio Komori

ref.) One-dimensional self-organized patterns on vicinal Cu(001)-c(2x2)N surfaces, Jpn. J. Appl. Phys. 41 (2002) L1243-1246.

Self-organization of adsorbate-induced domains on solid surfaces has been one of the important subjects of nanoscale science. It has been shown that one- and two-dimensional nanopatterns can be made on surfaces by adjusting the coverage of adsorbates and adsorption temperature. On a nitrogen-covered Cu(001) surface, there forms a grid pattern consisting of c(2x2)N square patches of 5x5 nm2 and 2 nm wide clean Cu surface at half monoatomic layer coverage [1] as shown in Fig. 1(a). The surface was prepared by annealing a Cu(001) crystal to about 670 K in 5 min after the nitrogen ion irradiation on the surface at room temperature. This pattern formation is mainly attributed to the relaxation of the elastic strain due to the lattice expansion on the nitrogen-adsorbed surface. Here, the clean Cu surface and the monoatomic steps act as strain relievers although the role of the step is secondary for the formation of the grid pattern.

We have found that step density and direction drastically influence the formation of one-dimensional patterns on Cu(001)-c(2x2)N vicinal surfaces [2]. Figure 1(b) shows one-dimensional array of the N-adsorbed square patches on the surface vicinal to the [100] direction. In this case, the width of the terrace is fixed to the period of the grid pattern. On the surface vicinal to the [-110] direction, on the other hand, a labyrinth pattern is formed as shown in Fig. 2(a). Here, the lines of clean Cu surface are aligned along the <110> direction. The size and shape of the nitrogen-covered domains are inhomogeneous on the surface. The image in Fig. 2(b) shows the result of subsequent annealing of the sample in Fig. 2(a) for 5 min. The stripe domains parallel to the [110] direction occupy three times larger area than the domains with the stripe parallel to the [-110] direction, and small areas with the square patches coexist. We notice that there are short strips of clean Cu surface along <100> directions at the corners of two long clean Cu lines along <110 > directions.

Main characteristics of the stripe patterns can be explained by assuming an anisotropic expansion of the lattice at c(2x2)N surface; the lattice constant increases only along the direction perpendicular to the clean Cu lines while that along the Cu line remains the same. No strain reliever is necessary in the direction of the Cu lines while both the step edges and the clean Cu surface are the relievers in the perpendicular direction. The observed short strips of clean Cu surface end at the centers of the c(2x2) stripe domain, and never connect two clean Cu lines. In the present model, the short strips are formed only highly compressed surface at the corners consistently with the general formation mechanism of the clean Cu lines.

References

[1] F.M. Leibsle, C.F.J. Flipse and A.W. Robinson, Phys. Rev. B47, 15865 (1993). [2] S. Ohno, K. Yagyuu, K. Nakatsuji and F. Komori, Jpn. J. Appl. Phys. 41, L1243 (2002).

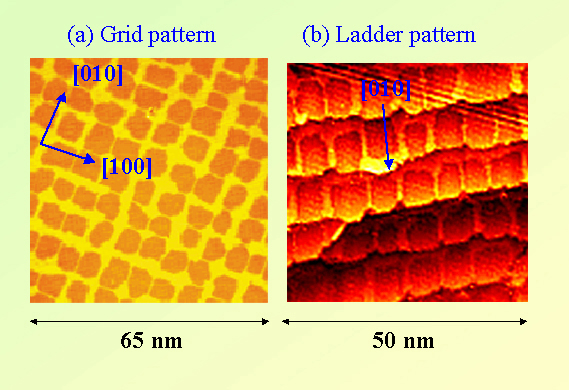
Figure 1(a) A square grid pattern of 7 nm period on a flat nitrogen-adsorbed Cu(001) surface. Clean Cu surface is imaged bright and c(2x2)N surface dark. Nitrogen density in this image is 1/4 of Cu surface atoms density on average. Sides of the square c(2x2) patches are along <100> directions. (b) One dimensional array of the square c(2x2)N patches on a N-adsorbed Cu(001) surface vicinal to [100] direction. Width of the terrace is quantized by the period of the grid pattern. Formation of these patterns is attributed to strain-relief on clean Cu surface and monoatomic steps.

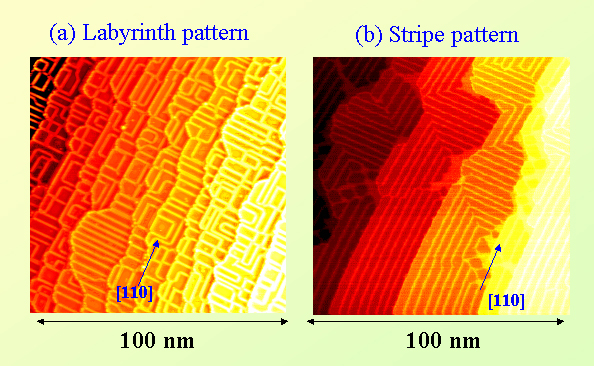
(a) A labyrinth pattern formed on a nitrogen-adsorbed Cu(001) surface vicinal to [110]direction. . The lines of clean Cu surface of 1-2 nm wide are along the <110> directions, and the@size and shape of the N-covered domains are inhomogeneous. (b) A stripe pattern on a nitrogen-adsorbed Cu(001) surface vicinal to [-110]direction. This pattern was obtained by annealing the surface in Fig. 2(a). The width of N- adsorbed stripe domain parallel to the [-110] direction is smaller than that parallel to the [110] direction. Small areas with the square c(2x2)N patches coexist.